
第4章 計算精度とパラメータ同定 -シミュレーション(CAE) の精度向上という根本問題ーその1
私が以前書いていた、はてなブログに本ページの原型となるいくつか記事があり、圧倒的にアクセス数の多いのが、「CAEの精度向上のためのパラメータ同定」というタイトルの記事です。いうまでもなく、シミュレーションは精度が命。程度の差はあれ、精度の保障なくては誰も使ってくれません。ところが、意外とどうすれば、実験と答えを合わせることができるのかという方法論を書いてある本やネット情報は少ないのです。要素技術的な情報はたくさんあふれていますが、このような使い方的ノウハウに属する情報はなかなか少ないのが現実なのでしょう。
2011年に書いたこの記事なのですが、いまだに、Googleで、”CAE 精度向上”で検索すると、なんとこの記事が一番上に来るんです。皆さん困っておられるのだと思います。書いた当人にとっては、世の中に少しは貢献できているようでうれしいです。自分でいうのもなんですが、この記事は精度を合わせるためのパラメータ同定の考え方をコンパクトにわかりやすく書いていると思います。どんな問題にも適用できる原理として書きましたので、実問題に適用するのもそれほど難しくはないはずです。キチンとした答えを出すには、その問題特有のクセと戦わなくてはいけなくて、そこが本当のノウハウになるわけですが。そこで、オリジナル記事を再編集して、本ページに2回に分けて掲載することにいたします。
もともとの発端は、別のあるブログへの、“解析の精度が不十分なために、設計変数の組み合わせによる応答値の傾向が変わってしまうという事はないのでしょうか。”という問い合わせに対して、“精度が不十分でも最適化技術は使えるのです”と回答したことでした。もちろん、実験値と不十分な合わせこみで済ませてしまうと、十分にあり得るリスクではありますが、そうしないためには、いくつかのケースで合わせこみを実施して、傾向も変わらないのはもちろん、精度もある程度保証される方法論が必要であること、そのためには、パラメータ同定という技術をしっかりと理解して活用することが大切であることを書いたのでした。
実験とシミュレーション結果の合わせ込み作業を、最適化アルゴリズムを駆使してたいへん効率よく行うことができるのです。シミュレーション(CAE)に従事される方にとっては、とても便利で根幹的な技法なのです。概念図も添付しましたので、それを見ながら読んでいただけるとわかりやすいです。
1.事前準備
次のようなモデルとデータを用意します。 A) 合わせる目標となる実験データ(これを、Rtと書きましょう。) 例えば、最大応力であれば、一個のスカラー値。振動問題であれば、周波数ごとの振幅のベクトル値になります。 B) 合わせる対象となるCAE解析結果(これを、Rsと書きましょう。) C) CAEモデル中の、精度を左右すると思われるパラメータを決める (これを、X1,X2, …, Xiと書きましょう。) 例えば、構造解析の場合、境界条件として与えるバネ定数の値など
2.基本的な考え方
1) 実験データとCAE解析結果の差分の絶対値を計算する。 Δ=|Rt−Rs| 2) 新しいXiについて、Rsを求め、1) に戻り、Δがゼロに近づくような、Xiのベストな組合せを見つける。 これは、目的関数Δを最小とする最適化問題を解く、と言い換えることができます。
そうなのです、原理はたったこれだけの考え方なのです。もちろん、あくまでも基本なので、応用的な考え方や注意点もたくさんありますが、原理原則はこれだけです。Xiを通常の設計変数と同様に扱い、上下限値を設定することで、Xiの設計空間を、実験計画法や最適化手法を使って探索するという方法を取るわけです。Δがゼロに近づくということはすなわち、実験データと合致するCAE解析結果が求められるということになるわけです。こういう定式化をしてしまえば、最適設計支援ソフトであっという間に、Xiを探索することができます。下記の例に示すように、パラメータ同定のニーズがあまりにも多いので、私の会社のソフトでは専用のツールを用意しています。一時は、ユーザのほとんどが必ず導入するほど要望の高い人気のオプションでした。
3.例
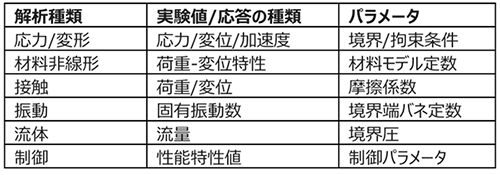
パラメータ同定の例は、解析の種類・問題の種類だけあるといっていいでしょう。シミュレーション結果の精度を確保せずに、設計に用いることはできませんから、当然のことです。下記にリストしたのは、一般的な例に過ぎません。
パラメータ同定の詳しい手順の事例 熱伝達率の同定方法及び焼き入れ時の構造計算方法 特許申請の一部なので、分かりやすいとは言えないのですが、厳密にしくみを理解するためには、いい情報かと思います。なかなかこの手の情報には巡り合えません。 http://www.ekouhou.net/熱伝達率の同定方法及び焼き入れ時の構造計算方法/disp-A,2010-127651.html
ーその2に続く 【SIMULIA 工藤】
バックナンバー
【デザインとシミュレーションを語る】第一回:イントロダクション 【デザインとシミュレーションを語る】第二回:シミュレーションの分類 【デザインとシミュレーションを語る】第三回:シミュレーションは実験と比べて何がいい? 【デザインとシミュレーションを語る】第四回:シミュレーションは緻密な統合技術 【デザインとシミュレーションを語る】第五回:リアルとバーチャルの垣根をなくせたら?(1) 【デザインとシミュレーションを語る】第六回:リアルとバーチャルの垣根をなくせたら?(2) 【デザインとシミュレーションを語る】第七回:3D-CADは何のため? 【デザインとシミュレーションを語る】第八回 : CAE を志す人へのメッセージ(1) 【デザインとシミュレーションを語る】第九回 : CAEを志す人へのメッセージ(2) 【デザインとシミュレーションを語る】第十回: ソフトウエア・ロボットの誕生 【デザインとシミュレーションを語る】第十一回: 作業を自動化すること、その真の価値とは 【デザインとシミュレーションを語る】第十二回: “自動化を進めると設計者が考えなくなる?"への回答 【デザインとシミュレーションを語る】第十三回 : パラメトリック性の本質は新しい組み合わせ 【デザインとシミュレーションを語る】第十四回 : Zero Design Cycle Timeの衝撃 【デザインとシミュレーションを語る】第十五回 : 「設計とは最適化」の奥深い意味を教えてくれた技術者 【デザインとシミュレーションを語る】第十六回 : スーパーコンピュータで行われていた大量の計算とは 【デザインとシミュレーションを語る】第十七回 : 最適設計支援ソフトウエアの衝撃的な登場 【デザインとシミュレーションを語る】第十八回 : サンプリングって、偵察のことです 【デザインとシミュレーションを語る】第十九回 : 設計空間でシミュレーションを考える 【デザインとシミュレーションを語る】第二十回 : 安易に使うと誤解を招く言葉“最適化 【デザインとシミュレーションを語る】第二十一回 : 世の中すべてはトレードオフ問題 【デザインとシミュレーションを語る】第二十二回 : Optimization、Trade-off、Synthesis 【デザインとシミュレーションを語る】第二十三回 : 最適解は失敗の学習結果 【デザインとシミュレーションを語る】第二十四回 : ”設計とは逆問題”のココロは?(1)-森を見る利点 【デザインとシミュレーションを語る】第二十五回 : ”設計とは逆問題”のココロは?(2)-解空間から設計空間を絞り込む 【デザインとシミュレーションを語る】第二十六回 : 100倍性能の高いコンピュータがあったら?―森と木の視点

