【第８章 複雑性設計に対応する】68: 複合領域シンセシス
ダッソー・システムズの工藤です。このページでなんどかトレードオフ問題について書きました。設計は、いや世の中の問題は、すべからくトレードオフ問題に対する多目的意思決定(Multi-Criteria Decision Making)が関わっています。
複合領域最適化は、“不必要な擦り合わせ”を解消する技術と言えるでしょう。トレードオフ問題を非合理的/非効率な調整によってではなく、合理的に一度に判断できるのです。設計は工学的な性質を判断しているわけなので、本質的に合理的な判断ができるはずなのですが、複数の専門家が介在していたり、調整や専門外の判断ができない、情報に整合性がない、その場で確認できない、といった理由により、設計レビューの時点で、合理的な判断が阻害されているというのが設計で起きている問題の根源なのです。より普遍的な言い方をすれば、判断を下すための情報不完全性です。
もちろん、100%完全な情報を得ることはできませんが、複合領域最適化は、本質的にこれらの課題を可能な限り最大限に解決しうる手法なのです。英語では、Multi-Disciplinary Optimization (MDO)という言葉がポピュラーになっているので、つい、複合領域最適化と言ってしまいますが、実際には、最適化というより、合理的な調整、すなわちシンセシスと云った方がしっくり来るように思います。ですので、タイトルにはシンセシスとしました。これまで説明してきかことを、わかりやすい絵でかいてみたのが、添付の絵ですね。イメージ伝わりますでしょうか。
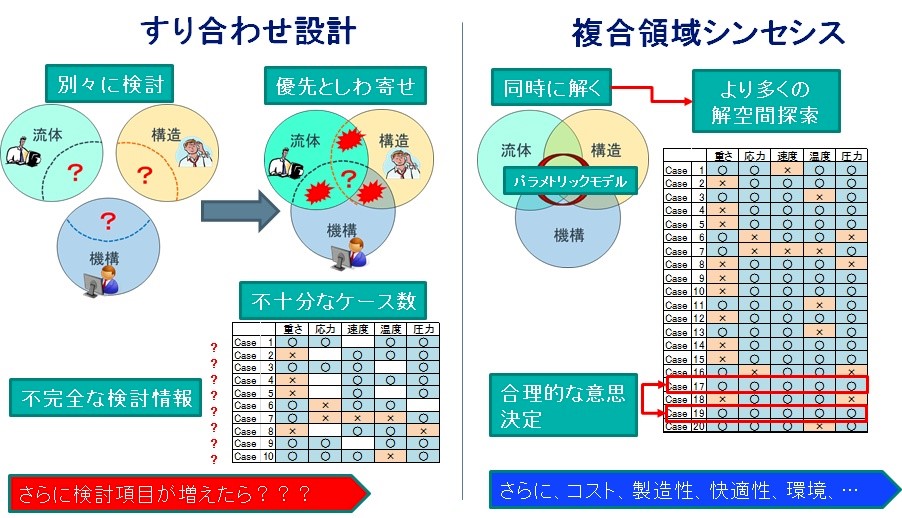
それでは、Before/Afterをもう少し詳しく見てみましょう。まず、Before-従来型（あるいは、今日型と言ってもいいでしょうか）の状況はこうです。たとえば、強度を評価する専門家、流体性能を評価する専門家、機構を考える専門家それぞれは、同じ製品のCADモデルから、おのおの構造解析モデル、流体解析モデル、機構解析モデルを作成し、専用解析ソルバーで性能計算をします。その時、おのおのが関心がある性能に影響する設計変数についてのみ、個別に検討することになります。このとき、変更検討した設計変数が、他の性能に影響を及ぼさない（独立に検討できる）のであれば、後で確認するだけで何ら問題は起きません。
問題は、誰かが変更検討した設計変数が他の性能に影響を及ぼすかもしれないという場合で、その変更情報を伝えて、悪い影響を与えていないか確認してもらう、その結果ダメ出し回答が来るかもしれません。そうすると、再度別の検討案を出さないといけなくなります。こういう設計変更の行ったり来たり状態を、モグラ叩きとよく言われます。そういう状態を何度も続けることはできませんから、担当者同士での”擦り合わせ”が行われるわけです。言ってみれば、もっとも影響が少ない範囲である種の妥協を行うということです。たとえば、想定よりも重量が重くなる、形が恰好悪くなる、部品が増えるなど、どこかにしわ寄せがきてしまう解決方法を取らざるを得なくなるのです。数学的に表現すると、設計変数の組み合わせ[X(i), i=1,L]に対する、性能変数[Y(j), j=1,M] の結果の情報がすべて得られていない（情報不完全性）ということです。（参照図の左側の表）
では、Afterである複合領域最適化を行うとどうなるのでしょうか。原理は、このページで何度もお話した、パラメトリックモデルの構築にあります。前述した、「同じ製品のCADモデルから、おのおの構造解析モデル、流体解析モデル、機構解析モデルを作成し」というのは同じですが、これをすべてのモデルがパラメトリックに自動生成できる技術を構築することが前提となります。この時点で、おそらく多くの方々は、そんなの無理！複雑な製品でできっこないと、考えるでしょう。もちろん、あらゆる製品に適用できるものではありませんが、例で示すと、航空機の機体まるごと（内装含む、エンジン詳細除く）、ジェットエンジン丸ごとの、概念設計～基本設計パラメトリック・モデルを、大手各社はすでにその構築技術を持っています。自動車においても、車体丸ごとのパラメトリック・モデルも設計変数は限定されていますが、いくつか事例は出ています。
さて、パラメトリック・モデルができてしまえば実は、あとは手順としてはとても簡単なのです。Isightをはじめとする自動実行と最適設計アルゴリズムを持つ市販の最適設計支援ソフトを使えば、サンプリングや最適化アルゴリズムで指定された設計変数の組み合わせX(L)に対して、性能変数Y(M) の結果がすべて求められるということです。設計変数と性能変数の行列情報がすべて埋められるということです。（参照図の右側の表）原理的には、製造性、コストなど一見すると設計の初期段階では考慮するのが難しい性能指標であっても、製造条件を定量的に表現でき、コスト・エンジニアリングによりコスト計算ができれば、設計段階のワークフローの中に組み込むことができます。設計変数の行列情報＝設計空間、と性能変数の行列情報＝解空間、がわかってしまえば、あとは制約条件を考慮し、重量最少、性能最大、トレードオフなどを考えて、円滑かつ合理的に意思決定を行うことができます。複合領域シンセシスと称している理由がおわかりいただけたでしょうか。
最後に前回“67:シミュレーションをつなげる方法を整理する”で説明したつなげる方法との関連で説明しましょう。複合領域問題が、性能領域間で直接の結果依存性がないので、検討は独立にできる場合であっても、モデルの変数変更を介在して、間接的にお互いに影響しあうことになるわけなので、複合領域シンセシスの考え方は必須です。ほとんどの設計問題はこのケースですが、性能シミュレーションごとのモデルを同等粒度・精度で作る必要があるので、その点が技術的なバリアになります。
一方、弱連成（ある性能の結果を使って、次の性能計算を行う）の場合は、たとえば、流体からの圧力による応力計算、電流による発熱と熱応力などのように、連成して解くのが当然の場合は、複合領域技術のみが、正しい解決策となります。特に、連成性が強連成ほど高速な現象ではないものの動的に変化する場合や非線形的であったりすると、きちんと連成して解く方法しかなくなるのです。わかりやすい例としてロケットの再突入シナリオを考えてみます。まず突入軌道が計算され、その速度と空気密度で流体計算がなされ、空気との摩擦熱による熱計算、空気圧による強度計算が行われます。それらが時々刻々と変化していく過渡的な現象はすべてを連成させて解かなくてはならないので、本質的に複合領域・多目的問題となります。この問題を1セットとして、軌道が変化した場合のロバスト性・信頼性を評価する場合にはさらに、これらの計算をモンテカルロ法で数百回も計算する必要があります。情報は少し古いですが、下記のその問題の概要を見ることができます。
Designing-in Certainty in an Uncertain World
【DASSAULT SYSTEMES 工藤啓治】
工藤はCAE分野で39年の経験を持つエキスパートとして、CAE開発・販売、HPC活用・マーケティング、最適設計・ロバスト設計市場開拓などを経験し、現在はシミュレーションを活用した設計業務改革コンサルと自身のノウハウ形式知化に取り組んでいます。