【デザインとシミュレーションを語る】37 : タグチメソッドとシックスシグマ手法の使い分け

第5章 不確定性を掌に置く　【タグチメソッドとシックスシグマ手法の使い分け】

今回のテーマは、同様タイトルで簡単な論文にしたものを元にしているので、少し難易度高いかもしれません。まとめを多少書き直しただけですので、途中？？？の方は、差異のところを飛ばして、最後の「推奨される適用場面」をお読みいただければ結構です。

· 元論文：「DFSSとタグチメソッドの使い分けに関する一考察」　計算工学講演会論文集　Vol.19 (2014年6月）

ロバスト設計は、シミュレーション技術の広がりと、手法の認知、技術の成熟化により、この10数年で実用化領域が広がってきています。DFSS(Design For Six Sigma)とタグチメソッドの二つの手法がよく使われているものの、その歴史的経緯、定式化、用語、指標、アプローチなどの違いが大きいため、技術者だけではなく会社によって、使う手法が分かれているのが現状なのです。この状況は、長らく知られてはいたものの、触れることが難しいテーマであることと、技術者同士の垣根が高く相互交流がないことから、どのように使い分けるかといったところまで踏み込んだ議論は、これまで十分になされてこなかったように思われます。今回、ロバストな製品を設計するという共通の目的を持つ両手法の特徴を踏まえたうえで、どちらか一方ではなく、場面に応じて使い分けをすることで、より高度なロバスト設計を行うことができるのではないかという問題提起を行ってみましょう。

DFSSとタグチメソッドの主な差異

両手法にはさまざまな点で差異がみられますが、視点を変えれば、得手不得手が存在するということなので、それを把握することで、効果的な利用方法を想定することができます。以下の説明では、タグチメソッドを、TMと略記します。

(1)　共通目的 製品の製造工程や利用時には“制御できない”不確定性すなわち、バラツキ（誤差）が生ずる。材料物性、熱加工変化、溶接、加工公差、組み付け公差、環境温度や圧力、運転条件などの誤差が生じたとしても、性能が安定する設計パラメータの組み合わせを求めるのが、ロバスト設計の目的である。

(2)　ロバスト性指標 【DFSS】　誤差分布を与えたときの性能のばらつきを、性能分布の標準偏差シグマ（σ）で表わし、シグマを小さくする（ロバスト）か、分布の平均値を安全側に移動させる（信頼度）設計点を探索する。 【TM】　ロバスト指標の目安としてSN比が使われる。SNは求める特性（望目、ゼロ望目、望小、望大、動特性）によって定義は異なるが、望目特性の場合には、平均値/標準偏差を最大化する設計点を探索する。信頼度指標はなく、あくまでロバスト性が主目的である。

(3) 設計変数 【DFSS】　連続値・離散値のいずれも扱うことができる。 【TM】　離散値のみを扱う。選択できる数値や尺度の組を、水準と呼び、２水準、３水準などで表現する。

(4) 手法概要 【DFSS】　誤差を正規分布などで想定し、モンテカルロ法や実験計画法といったサンプリング手法を実施し、性能の分布を求める。分布から、平均値や標準偏差等の統計値を求め、それらの指標の最適化（最大/最小）を行う。計算回数は、設計変数の探索回数ごとに、誤差のサンプリング回数を実施することとなるので、掛け算した計算回数を要する。

【TM】　直交表（実験計画法）で制御因子と誤差因子（制御因子が加わる場合もあり】の組み合わせを設定し、P-Diagramを構築する。静特性の場合は制御因子x 誤差因子の直交表の掛け算、動特性の場合はさらに、制御因子直交表を掛けた回数の計算を要する。

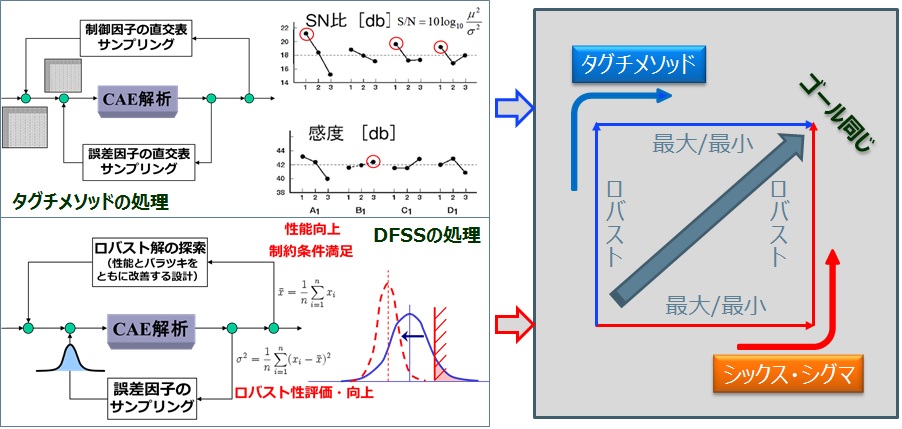
(5)　目的へのアプローチ 【DFSS】　通常は、誤差を想定しない設計空間のみで最適解探索を実施する。その設計点を初期値として、誤差分布を与え、ロバストもしくは信頼度の高い設計点を探索するという手順を取る。最適解探索の時点で誤差分布も考慮してしまうと、計算回数が膨大になるためである。 【TM】　設計空間探索時に同時に誤差因子での計算もしているので、S/N比を最大化する（ロバスト）設計点を先に求める。その後、平均値だけに影響を及ぼす設計因子の水準を選択しチューニングを行うという、いわゆる「2段階設計」のアプローチを取る。

(6)　制約条件 【DFSS】　計算時に陽的な形で取り扱うことができる。 【TM】　計算を終え要因効果図を用いて二段階設計を行うときに、利用者が判断する。

(7)　判断 【DFSS】　計算終了時にはロバスト設計点が求められているので、結果の確認で十分である。 【TM】　計算終了時に、最もロバストな制御因子の組み合わせは求められているが、組み合わせによっては直交表に含まれていない場合があるので、確認のため実計算を実施する必要がある。最終的な組合せの判断は利用者が行う。

(8)　長所 【DFSS】　連続変数をそのまま扱えるので、非線形性の高い問題にも適用しやすい。制約条件を考慮しての信頼性指標も含んだ明確な問題設定ができる。複数の目的関数や制約条件を考慮した複雑な問題に適用できる。 【TM】　実験計画法をベースにしているので、間隔や順序を表す尺度だけではなく、ケースや条件などの名義尺度を水準として使うことができ、適用問題の範囲が広い。

(9)　計算回数の課題 【DFSS】　設計変数の探索回数ごとに、誤差のサンプリング回数を実施するので、計算回数が多くなる。 【TM】　動特性に適用する場合、シグナルの水準数が多くなると、総計算回数が増える。

推奨される適用場面

（１）構想設計段階でのロバスト性評価 構想設計においては、設計変数が多く、上下限値も広いケース、すなわち設計空間が広い場合が多いわけです。直交表を活用したタグチメソッドであれば、広い設計空間でも、水準数を調整しながら計算回数を抑えてロバスト性の評価をすることができ、適用場面が広いと言えます。また、構想設計時には制約条件を厳しく課すよりも、ざっくりとして傾向を把握したい場合も多いので、タグチメソッドに有利です。さらに、後工程での変化する可能性のある制約変数（重量など）を、誤差因子に含めて検討することで、後工程でのリスク影響の少ないという意味での、ロバスト設計にも適用することもできます。

（２）詳細設計段階でのロバスト性および信頼性評価 詳細設計段階では、多くの場合設計空間は絞られています。また、制約条件を厳しく満たす必要も求められるでしょう。DFSSが効果を発揮するのは、このような、比較的狭い設計空間で、制約条件を満たしながら、ロバストでかつ、目的関数が最小もしくは最大であるような、複雑な問題設定での設計点を探索するといった場面になります。特に、バラツキを考慮しない（決定論的）最適解探索がすでに終了しており、その設計点の周りでロバストでかつ信頼性の高い設計点を求めたいという場合には、最も効果を発揮します。計算回数が膨大になる場合には、近似モデル（最近は、近似という言葉を嫌い、“代理モデル (Surrogate Model)”と呼ばれることが多い。）を利用する方法が取られる場合も多く、設計空間が比較的狭ければ、モデルの精度も隠しやすいことからも、有利な活用方法になります。

まとめ

DFSSとタグチメソッドを使い分けるという視点で、差異を整理し、その効果を発揮しやすい適用場面をまとめてみました。これまでは、ともすると、（創始者が日本人で、日本的発想だから）日本向きとか、（アメリカの発想で開発され、絨毯爆撃的なので）欧米流といった偏った見方をされるきらいのあった、タグとメソッドとDFSSを客観的に比較してみようと試みたものです。目的は共通でありながらその思想とアプローチが異なるので、どちらがいいかではなく、状況を踏まえて使い分けることがふさわしいというのが結論となります。これらの手法がより広く深く認知されて、実設計でますます活用されることを願って。

【SIMULIA　工藤】