第5章 不確定性を掌に置く 【ロバスト設計の価値と方法論】
ロバスト設計を平たく言うと、”製造や使用条件にバラツキがあっても、製品がブレずに安定した性能を出すことができるようにする設計”ということになります。一見すると、当たり前のことで取り立ててすごい技術だとかいう必要はないように見えますが、実は、最後に”設計”と書いてあるところがミソです。その意味を明確にするために、モノを作る使う上で、ばらつきが生じていることへの対応には以下の4つがあることを理解する必要があります。
① 無視する
すべての量にはバラつきがあるわけですけれど、もちろん大概のものは影響が小さいので無視できるのです。無視できないけれども、あえて平均値だけを扱うのが決定論的アプローチで、通常のシミュレーションは最適設計も含めて、この意図的な無視をしているわけです。無視できない場合には、以下の対策を行います。
② 誤差を制御する
加工精度を上げる、品質の高い材料を使う、機械でなく人が仕上げる、さらに熟練者が仕上げるなど製造時の対応です。品質は上がるものの、基本的にコストがかかります。
③ 誤差の影響を補正する
不良をはじくという品質検査や、使用条件を厳しくすることで、不具合を出にくくするなど、製造後の対応です。品質を上げているわけではなく、品質が悪いものを出さないという処理なので、歩留りが悪いことによる廃棄や検査工数などにより、やはりコストはかさみます。
④ 誤差の影響を最小化する
誤差は制御できないという前提に立ち、誤差があったとしても。その影響が出にくい設計を行うという、これがまさにロバスト設計手法です。製造前に対処できるわけなので、これの方法がもっともコストがかからず、製造への負担とコストも減らす方策なのです。
②と③のように、誤差を制御したり補正したりするのは、製造に入ったあとの対応であるのに対し、④のロバスト設計は言葉の通り、製造前である設計段階でしかるべき手を打つという原則なのです。優秀なエンジニアとシミュレーション環境を揃えればいいだけですから、製造以降の対策コストや不良品排除のコストに比べれば桁違いに少ないですし、それを不要にしてしまおうというこのなので、二重の意味でコスト削減と期間短縮に寄与できるのです。しかも、シミュレーションといっしょに活用することで、実現可能な手法であるところが、さらに深い意味と可能性を与えます。
ですから、ものづくりに従事している方々にとっては、いいことづくめで、とても重要な技術のはずなのですが、シミュレーションを活用したロバスト設計が本格的に実施されだして以来20年も経つのに、意外と広がりが少ないと感じるのは、技術の敷居が高いせいでしょうか。方法論が浸透していないせいでしょうか。
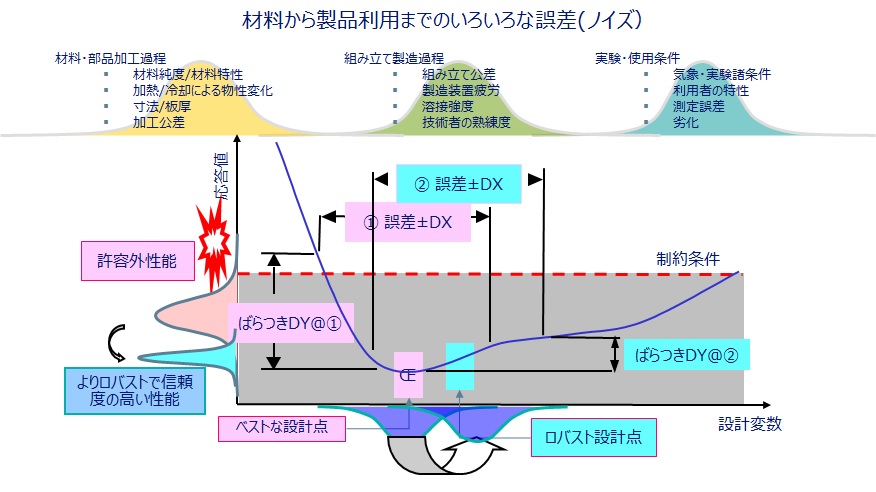
次に、本題となる、ロバスト設計を実施するための基本的な考え方を5つのテーマに分けて説明します。
（１）何の誤差を想定すればいいのか？
この問いに明確な答えはありません。ある量（厚さ、寸法、材料など）の誤差の影響があるかないかは、結果的には経験則の積み重ねです。たとえば、公差がどういう基準で決まっているかは、過去知見による社内設計ルールであると、よく言われます。ただし、それを検証する方法はあります。幾つかの変数に誤差の幅を与えてシミュレーションすることで、影響度合いを比較するのです。また、誤差の幅を意図的に変更することもできます。それにより、どの量の誤差が、どの程度までであれば、性能に影響を及ぼす度合いが大きいか、小さいかを把握することができます。ヴァーチャルで事前検証できる価値の一つです。
（２）誤差を定量的に表現するには？
定量的に正確な表現には分布関数が必要です。誤差を考えるので、統計的世界になるのです。普通は正規分布を考えれば十分ですから、一つの量は平均値と標準偏差をいう二つのパラメータで定義できてしまいます。シックス・シグマを使う場合にはこれでOKです。一方、タグチメソッドの場合は、分布関数ではなく、標準偏差と同等の変化量として、水準という定義を用います。要は、数値のバラツキであれば、低‐中‐高の３水準、ケース分けのような場合には、A‐B-Cの３水準、分岐条件の場合は、あり‐なしの2水準といったように、ざっくりとした離散値の組み合わせで考えますので、変数の適用範囲が幅広いのが大きなメリットです。
（３）誤差による影響をどうやって評価するのか？
正規分布の誤差（たとえば、寸法公差や材料定数のバラツキ）を入れて、構造解析であれば応力とか、熱問題であれば温度といった応答値の分布を得るには、”分布”を表現できる十分なだけの回数のシミュレーションを実行します。たとえば、100回の誤差分布計算から100個の応答値を得て、分布の平均値と標準偏差を求めます。この標準偏差を小さくするような、設計変数の組み合わせを探すのが、ロバスト設計の方法です。ところが、これを設計変数の一組について行わないといけないので、仮に200パターンの組み合わせでの標準偏差を求めようとすると、二重ループの計算となり200 x 100 = 20,000回のシミュレーションを実施することになります。（５）に示すように、計算時間の壁を解決しないといけないのです。
（４）どういう基準と方法で、”安定した性能”を導くのか？
先の例でいうと、200パターンの設計変数の組み合わせの中で、もっとも標準偏差の小さいもの＝ばらつき分布幅小さいものが、もっともロバストであるということになります。しかし、性能が劣ってしまっては、いくらロバストでも意味がなくなってしまいますので、実際の設計においては、性能を維持、できれば改善しながら、許容される標準偏差に収まるロバストな設計ポイントを求めることが要求されます。言い換えれば、性能最適化とロバスト化のトレードオフ問題を解くことになるのです。（ロバスト性の代わりに、信頼性を指標にする場合もあります。）
シックス・シグマ手法であれば、性能の平均値最大化もしくは最小化と、標準偏差との多目的最適化問題で解いたり、（標準偏差の倍数である）シグマ値を制約条件にして単目的性能の最適化で解いたりと、いろいろな手立てがあります。タグチ・メソッドの場合であれば、S/N比最大化と感度による性能調整という手順を取ります。さらりと数行で書きましたが、ここの取り扱いと考え方は、どちらの手法にとっても、評価の要になる解法戦略にあたる部分です。別途書こうと思います。
（５）計算時間という壁の克服
先の例だと、最適解の探索も行うと200パターンでは済まず、数百数千回の組み合わせが必要となる場合もあり、これを実施するには、通常の方法であれば膨大な計算時間を要することはすでに書きました。計算時間の膨大さを解決するには、”近似モデル（Approximation model)”を利用します。最近では、”近似”というと誤解を招くので、”代理モデル（Surrogate model)”と称する場合が見受けられます。この技術を構築するには高度なシミュレーション、最適設計、ロバスト設計、統計知識などが要求されます。そういう意味ではちょっと敷居が高くなってしまうのは、ある意味仕方のないことではあるのですけれど、それを乗り越えた先には、素晴らしい世界が待っているのです。たくさんの事例がありますので、折に触れて紹介できればと思います。
さてさて、数式は使わないものの、専門用語たっぷりになり過ぎてしまいました。ここらへんのテーマが一番難解に感じられるところかもしれませんが、この峠を越えていただくと、また見通しが少し広がってきますので、少し我慢してお付き合いいただけるとありがたいです。
【SIMULIA 工藤】
工藤はCAE分野で39年の経験を持つエキスパートとして、CAE開発・販売、HPC活用・マーケティング、最適設計・ロバスト設計市場開拓などを経験し、現在はシミュレーションを活用した設計業務改革コンサルと自身のノウハウ形式知化に取り組んでいます。