【デザインとシミュレーションを語る】28 : シミュレーション（CAE) の精度向上という根本問題ーその２

第４章　計算精度とパラメータ同定　－シミュレーション（CAE) の精度向上という根本問題ーその2

その1の続きの記事となります。

４．注意点

１）適用していい場合とよくない場合

適用していいのは、

A) 実験データが信頼できる B) シミュレーションの結果が信頼できる シミュレーション・プログラムや計算アルゴリズムが信頼できる（＝成熟している） 形状を正しく追従しているとか、メッシュ粒度が十分など、モデルの本質的な部分は信頼できる（＝正確である） C) 実験とシミュレーション結果が合わないのは、モデル中の定数や条件が不正確なためである

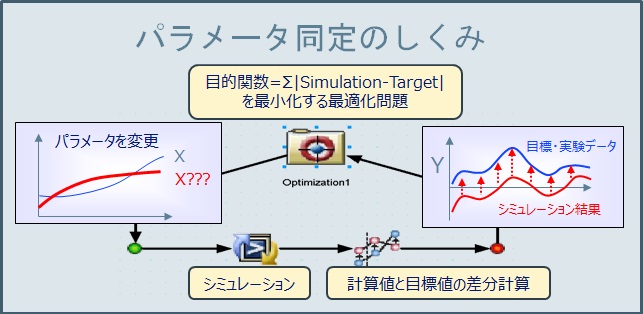
という前提が成り立つ場合です。定数や条件を決めるパラメータを正確に求められれば、結果も合うはずであるという論理が成り立ちます。これは一見当たり前の用に見えると思うのですが、実際は下記のやってはいけないことと区別がつきにくいことも多いのです。

D) 実験の測定誤差や想定していた条件と異なる可能性 E) シミュレーション・プログラムやアルゴリズム自体に不安定性や精度不足がある F) モデルの本質部分がいいかげんなのに、見当違いのパラメータで無理やり合わせようとすること

特に、シミュレーションの現象とモデルのことを熟知していないと、上記の（F)のミスに気付かない場合もありがちです。これをやってしまうと、ケースごとに同定値が異なるというような明らかにおかしな出来事が起こるはずです。

２）正しいパラメータを選ぶということ 選択したパラメータを上下限値の空間内で探索しても、Δが期待するようにゼロに近づかないということも出て来るでしょう。その場合は、パラメータの選択に誤りがあるか、探索空間が不十分であることを意味します。これはこれで、有用な情報になりますから、改めてパラメータの探索条件を設定し直して、再度試みればいいわけです。このようなケースをあらかじめ想定しておくには、何度もこのブログで書いていることですが、いきなり最適化手法を試みないことです。実験計画法を使って、どのパラメータが、今回の実験データへの合わせこみに寄与しているのかを、定量的に把握するということが、モデル精度について理解するのにとても重要なことです。最適化結果から得られた最後のパラメータの組み合わせだけを嬉々として得たとしても、その場限りの値を得たという以上の意味はないのです。

３）複数ケースで同定を行い、モデルとパラメータ選定が正しいことを検証 さて、実験データ1ケースだけで同定できても喜んではいけません。1ケースだけだと、偶然に、あるいは無理やり合わせこむことができるからです。いくつかのパターンの異なる実験データとも合うのでなければ、素性の良い同定パラメータとは言えません。実験データのたびに、値を変えなければいけないパラメータだとしたら、それは間違ったパラメータを選んでいることになります。この作業は、自分の作成したCAEモデルを理解するのにとても大切です。なるべく多くの実験パターンで使えること、パラメータに冗長性があることが望ましいと言えます。 例えば、二つのケースで同定を行うと、どちらか一つだけで同定するとかなり精度が出るけれども（例えば、5%以内）、おのおのの同定値が微妙に異なるという場合が出てきます。今度は、パラメータを同じ値にして、両方同時に同定しようとすると、二つとも精度を妥協せざるを得ないが、そこそこ合う。（例えば、双方とも、10％以内にはならない。）というような状況に遭遇するでしょう。この場合、精度は甘いかもしれないけれども、二つのケースに対しては同程度の追従性があると言えますから、それを理解したうえで、決められた同定パラメータで、以降最適設計を実施するということが可能になるわけです。 このパラグラフでの説明が、冒頭のご質問への回答ということになります。

５．応用

この手法にはすばらしい応用があります。二つ示しましょう。

１）目標値への合わせこみ すぐにわかることですが、実験データを目標データに置き換え、同定パラメータを本来の設計変数に置き換えれば、目標特性を実現する設計変数を求める最適化問題にすることができます。エンジン性能の低回転から高回転までの性能や燃費の理想特性カーブを設定し、そのカーブに近づくエンジンの設計パラメータを求めるという典型例があります。

２）1Dモデルのパラメータ決定 最近1D-CAEが注目を浴びています。3次元の複雑な現象を、1次元化された方程式とモデルに置き換える手法です。近似モデルの一つということもできますが、概念設計段階では詳細な形状は設定されていませんし、主要な諸元を決定することが目的なので、1D-CAEが大きな役割を果たすのです。その際に重要なのが、3次元形状に依存する現象を、1Dモデルで表現するための素性の良いパラメータです。例えば、

素性の良い1Dパラメータを求めるために、3Dモデルの結果を目標値にして、1Dモデルの結果を合わせこむという方法がとても有効になるわけです。

６．シミュレーションの品質保証に関する議論

シミュレーション結果の精度の問題は、シミュレーション屋にとっては常に付きまとう問題です。この仕事をやっている限りは、ある意味で精度との戦いをやっていると言っても言い過ぎではないと思います。方程式の正しさから始まり、離散化、近似、理想化や仮定、材料モデルなど精度を阻害する要因は、シミュレーション技術の中には無数にあると言っていいでしょう。 日本学術会議の、「計算科学シミュレーションと設計工学分科会」から、シミュレーションの品質保証をテーマにした報告書「ものづくり支援のための計算力学シミュレーションの品質保証に向けて」が公開されています。精度だけではなく、より広範な品質という観点からのまとまった記述ですので、この業界の一般常識として一度目を通す価値はあるかと思います。（不肖私も端っこで参加しております。） https://blog-assets.3ds.com/uploads/2022/03/kohyo-21-h123-2-1.pdf

さらに、インターネットで、“シミュレーション　品質保証”で検索しますと、関連情報がたくさん出てきます。さて、「CAEの精度向上のためのパラメータ同定」の技法がとても役に立つだけではなく、CAEモデルの本質を理解するための手段でもあること、興味深い応用もあることが、おわかりいただけましたでしょうか。この作業を経たあとに、本来の設計最適化に着手することができるわけです。今回の記事はとても長くなりましたが、お役に立てれば幸いです。

【SIMULIA 工藤】

バックナンバー

【デザインとシミュレーションを語る】第一回：イントロダクション 【デザインとシミュレーションを語る】第二回：シミュレーションの分類 【デザインとシミュレーションを語る】第三回：シミュレーションは実験と比べて何がいい？ 【デザインとシミュレーションを語る】第四回：シミュレーションは緻密な統合技術 【デザインとシミュレーションを語る】第五回：リアルとバーチャルの垣根をなくせたら？(１) 【デザインとシミュレーションを語る】第六回：リアルとバーチャルの垣根をなくせたら？(２) 【デザインとシミュレーションを語る】第七回：3D-CADは何のため？ 【デザインとシミュレーションを語る】第八回 : CAE を志す人へのメッセージ（１） 【デザインとシミュレーションを語る】第九回 : CAEを志す人へのメッセージ（２） 【デザインとシミュレーションを語る】第十回: ソフトウエア・ロボットの誕生 【デザインとシミュレーションを語る】第十一回: 作業を自動化すること、その真の価値とは 【デザインとシミュレーションを語る】第十二回: “自動化を進めると設計者が考えなくなる？＂への回答 【デザインとシミュレーションを語る】第十三回 : パラメトリック性の本質は新しい組み合わせ 【デザインとシミュレーションを語る】第十四回 : Zero Design Cycle Timeの衝撃 【デザインとシミュレーションを語る】第十五回 : 「設計とは最適化」の奥深い意味を教えてくれた技術者 【デザインとシミュレーションを語る】第十六回 : スーパーコンピュータで行われていた大量の計算とは 【デザインとシミュレーションを語る】第十七回 : 最適設計支援ソフトウエアの衝撃的な登場 【デザインとシミュレーションを語る】第十八回 : サンプリングって、偵察のことです 【デザインとシミュレーションを語る】第十九回 :  設計空間でシミュレーションを考える 【デザインとシミュレーションを語る】第二十回 : 安易に使うと誤解を招く言葉“最適化 【デザインとシミュレーションを語る】第二十一回 : 世の中すべてはトレードオフ問題 【デザインとシミュレーションを語る】第二十二回 : Optimization、Trade-off、Synthesis 【デザインとシミュレーションを語る】第二十三回 : 最適解は失敗の学習結果 【デザインとシミュレーションを語る】第二十四回 : ”設計とは逆問題”のココロは？（１）－森を見る利点 【デザインとシミュレーションを語る】第二十五回 : ”設計とは逆問題”のココロは？（２）－解空間から設計空間を絞り込む 【デザインとシミュレーションを語る】第二十六回 : 100倍性能の高いコンピュータがあったら？―森と木の視点 【デザインとシミュレーションを語る】第二十七回 : シミュレーション（CAE) の精度向上という根本問題ーその１