안녕하세요. 다쏘시스템코리아 SIMULIA 브랜드팀입니다.
본 포스팅에서는 굽힘하중 조건에서 연속체 요소(Continuum element) 종류에 따른 해석 결과 변형률/응력의 특징과 변형률/응력 결과의 정확도를 개선하는 방법을 안내해 드리겠습니다.
Abaqus는 다양한 종류의 Continuum element를 지원하고 있습니다. 대표적으로 그림 1.에 나타낸 C3D8R 요소의 경우 3차원 상에 8개의 노드와 1개의 적분점으로 구성된 Continuum element를 의미합니다. 이때 요소의 노드(Node) 개수는 노드의 자유도(구조해석에서는 변위, 회전)가 요소 내 도메인에서 보간되는 방식을 결정합니다. 1차 요소의 경우 요소의 각 모서리에 노드가 존재하며 2차의 요소의 경우 1차 요소에 배치된 노드 사이에 추가적인 노드가 존재합니다. 적분점(Integration point)은 요소의 강성과 질량을 계산하는 표본점(sampling point)을 의미하며 변형률과 응력이 계산되는 지점입니다.
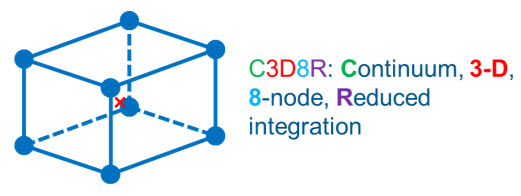
그림 1.
Continuum element 종류에 따른 변형률/응력 특징을 파악하기에 앞서 순수 굽힘하중 조건에서 빔의 물리적인 거동 및 특성은 아래와 같습니다:
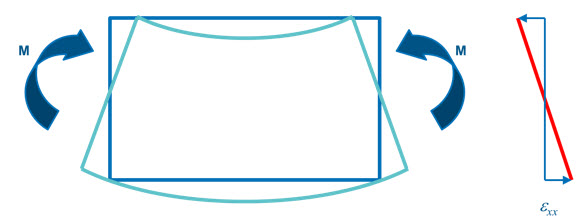 그림 2.
그림 2.
- 변형 중 임의의 위치에서 빔의 단면은 평면 형태를 유지합니다.
- 빔의 축방향 수직변형률(εxx)은 두께를 따라 선형적으로 변화합니다.
- 빔의 푸아송 비(ν)가 0인 경우 두께방향 수직변형률(εyy)은 발생하지 않습니다.
- 전단변형률(εxy)이 발생하지 않습니다. (변형되기 전 빔의 중심축과 평행한 라인은 변형 시 원호 형태인 것을 의미합니다.)
굽힘하중 조건에서 Continuum element 종류에 따른 해석 결과 변형률/응력의 특징과 변형률/응력 결과의 정확도를 개선하는 방법을 살펴보겠습니다.
1. Second-order solid elements(CPE8, C3D20R, …)를 이용하는 경우
: Second-order full-integration solid element 또는 Second-order reduced-integration solid element를 이용하면 굽힘을 정확히 모델링할 수 있습니다.
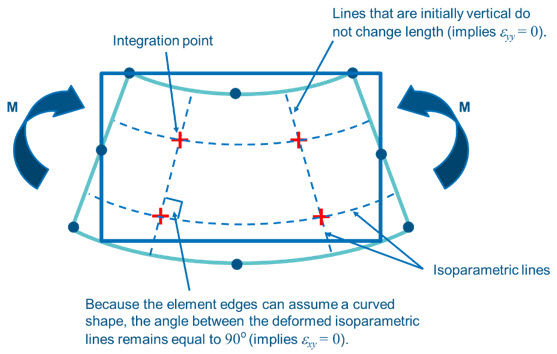
그림 3.
그림 3.에 나타난 바와 같이 2차 요소의 경우 각 노드에서 계산된 변위를 2차식 형태로 보간하여 적분점에서의 변위를 계산하기 때문에 적분점에서의 길이방향 라인을 곡선으로 나타낼 수 있습니다. 따라서 적분점에서 교차하는 라인 간 각도가 90°로 유지되는 것을, 결과적으로 실제 물리현상과 동일하게 전단변형률이 계산되지 않는 것을 확인할 수 있습니다. 따라서 Second-order full-/reduced-integration solid element를 이용하여 굽힘하중 조건에서 빔의 거동을 정확히 모델링 가능합니다.
2. First-order fully-integrated solid elements(CPS4, CPE4, C3D8, …)를 이용하는 경우
:물리현상과 달리 전단응력이 계산되어 실제 재료보다 강한(stiff) 거동을 띄는 shear locking 현상이 나타나기 때문에 굽힘이 지배적인 영역에서는 사용해서는 안 됩니다.
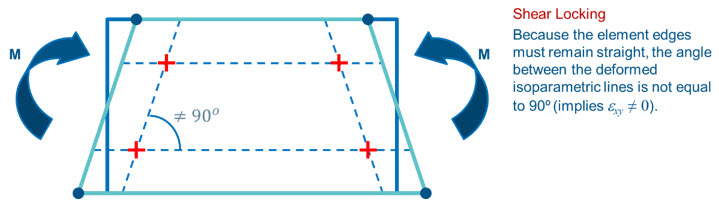
그림 4.
First-order fully-integrated solid element의 경우 적분점을 지나는 길이방향 라인의 변형을 직선 형태로 계산하기 때문에 적분점에서 교차하는 라인 간의 각도가 90°를 유지할 수 없게 됩니다. 따라서 실제 굽힘하중 조건에서 발생하는 물리적인 현상이 아닌, 수치적인 계산과정에서 element formulation에 의해 전단변형률(이른바 parasitic strain)이 발생하게 됩니다.
전단변형률은 요소 내 전단응력을 추가로 발생시키고 요소가 실제로 변형되어야 하는 상태보다 더 작은 변형이 발생한 상태에서 평형상태를 만족하게 합니다. 이러한 현상을 Shear locking이라 하며, 굽힘이 지배적인 영역에서는 First-order fully-integrated solid element를 사용하지 않아야 합니다.
다만 해석시간의 절약과 같은 이유로 인해 Second-order solid element가 아닌 First-order fully-integrated solid element를 사용해야 한다면 Incompatible mode element(CPS4I, CPE4I, C3D8I, …)를 사용해야 합니다. Incompatible mode element는 parasitic shear stress를 제거하여 굽힘 조건에서 요소의 거동을 향상시킵니다. 다만 요소에 과한 왜곡이 발생하는 경우 해석 결과의 정확도가 떨어진다는 점에 주의하여야 합니다.
3. First-order reduced-integration solid elements(CPE4R, …)를 이용하는 경우
: 요소의 변형은 발생하나 strain/stress가 발생하지 않는 hourglassing 현상이 나타날 수 있으므로 요소망을 촘촘히 구성하거나 hourglass controls을 사용해야 합니다.
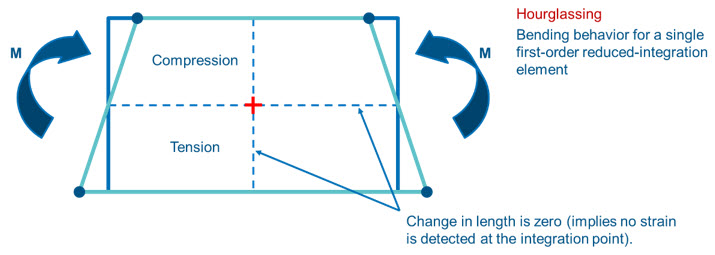
그림 5.
그림 5.와 같이 First-order reduced-integrated solid element의 경우 요소 중앙에 하나의 적분점이 존재하고 적분점을 지나는 라인의 길이가 유지되기 때문에 축방향 수직변형률(εxx)이 계산되지 않습니다. 따라서 요소의 변형은 발생하나 변형률이 발생하지 않는 zero-energy mode, 이른바 hourglassing 현상이 나타나게 됩니다(그림 6. 참조).
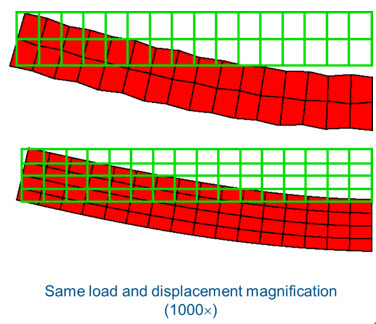
그림 6.
Hourglassing을 제거하는 방법은 아래 그림 7.과 같이 두께 방향으로 4개 이상의 충분히 많은 요소를 사용하는 것입니다. 여러 개의 요소를 이용한 경우 각각의 요소들이 인장 또는 압축 방향의 축방향 수직변형률을 잡아내기 때문에 hourglassing 현상을 개선할 수 있습니다.
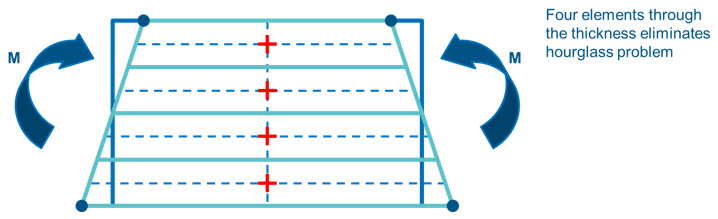
그림 7.
한편 요소 개수를 수정하지 않고 Built-in hourglass controls을 사용하여 hourglassing 현상을 개선하는 방법이 있습니다. 다만 해석이 완료된 후에 hourglassing을 제어하기 위해 사용된 artificial energy가 internal energy에 비해 충분히 작은지(<1%) 확인이 필요합니다.
그림 8.의 그래프는 두께 방향으로 2개, 4개의 요소를 구성한 후에 hourglassing control 기능을 이용한 결과를 비교하였습니다. 4개 요소로 모델을 구성한 경우 artificial energy가 internal energy의 0.1%로 계산되었으며 두께 방향으로 더 많은 개수의 요소를 사용하는 경우 hourglass 현상이 적게 발생하는 것을 확인할 수 있습니다.
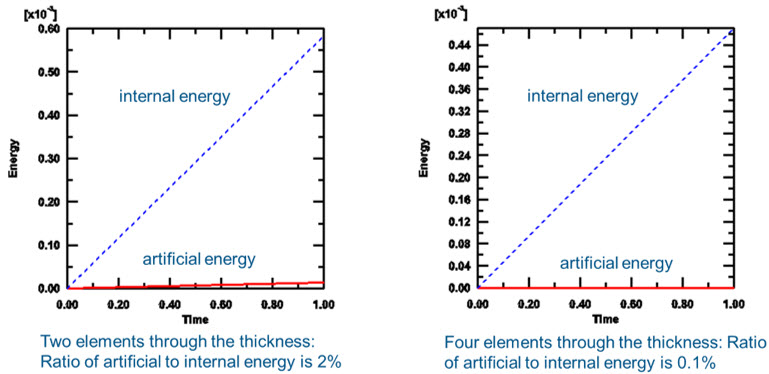
그림 8.
이번 포스팅에서는 굽힘 조건에서 continuum element 종류에 따라 계산되는 변형률/응력의 특징을 살펴보고 굽힘을 모델링하기 위해 적절한 요소 구성 방법을 살펴 보았습니다.
Abaqus를 이용한 해석과 관련하여 문의가 있으시면 SIMULIA 기술지원팀으로 연락 부탁 드립니다. (02-3270-8541, Simulia.kr.support@3ds.com)
