Reference
Zhu J, Wierzbicki T and Li W, 2018, A review of safety-focused mechanical modeling of commercial lithium-ion batteries, Journal of Power Sources 378, 153-168
Xu J, Liu B, Wang and Hu D, 2016, Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies, Applied Energy 172, 180-189
Reference
Zhu J, Wierzbicki T and Li W, 2018, A review of safety-focused mechanical modeling of commercial lithium-ion batteries, Journal of Power Sources 378, 153-168
Xu J, Liu B, Wang and Hu D, 2016, Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies, Applied Energy 172, 180-189
Reference
Zhu J, Wierzbicki T and Li W, 2018, A review of safety-focused mechanical modeling of commercial lithium-ion batteries, Journal of Power Sources 378, 153-168
Xu J, Liu B, Wang and Hu D, 2016, Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies, Applied Energy 172, 180-189
최근 환경규제가 심화됨에 따라 자동차 산업에 있어 전기차, 수소전기차와 같은 친환경 자동차의 필요성이 증가하고 있습니다. 전기구동 기반 자동차의 경우 배터리를 제외하고서는 논할 수 없는데, 주행 거리 증가를 위한 배터리 성능 향상과 더불어 배터리 안전성에 대한 요구 또한 증가하고 있습니다. 이에 따라, 개발 단계에서 시뮬레이션을 통한 전기차 배터리 성능 및 안전성 예측이 중요합니다.
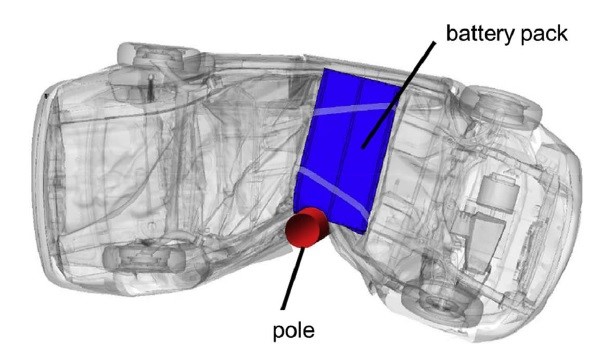
그림 1. 차량 측면 pole 충돌에 의한 배터리 팩 파손(Zhu. et al., 2018)
배터리 시뮬레이션을 위해서는 배터리 구조에 대한 상세한 모사와 배터리 물성에 대한 정확한 파악이 필요합니다. 그러나, 흔히 볼 수 있는 젤리롤(Jelly roll) 배터리는 양극재, 음극재, 절연체 등의 소재를 엮어 돌돌 마는 와인딩 공정으로 제조되는데 시뮬레이션 상에서 복잡한 구조와 재료층을 그대로 모사하는 것은 전처리뿐만 아니라 연산시간 측면에서도 굉장히 비효율적입니다. 실제 차량에 탑재되는 배터리 셀은 하나에 그치는 것이 아닌 수 백개에 달하기 때문에 이러한 문제는 해석 모델의 스케일이 커질수록 증대됩니다.
일반적으로 이와 같은 문제를 그림 2.에 나타낸 등가물성 개념을 도입하여 해결합니다. 풀어 말해, 여러 겹의 박막이 말려있는 구조를 일일이 모델링하지 않고 단순한 원통으로 모사하는 대신에 실제 젤리롤의 구조적 변형 상태를 대변할 수 있는 물성을 도출하여 사용하는 것입니다. 등가물성은 재료 항복 모델을 가정한 후, 실험 하중-변위 곡선을 활용하여 실험 결과와 해석 결과가 일치하도록 물성 파라미터를 보정하여 도출됩니다.
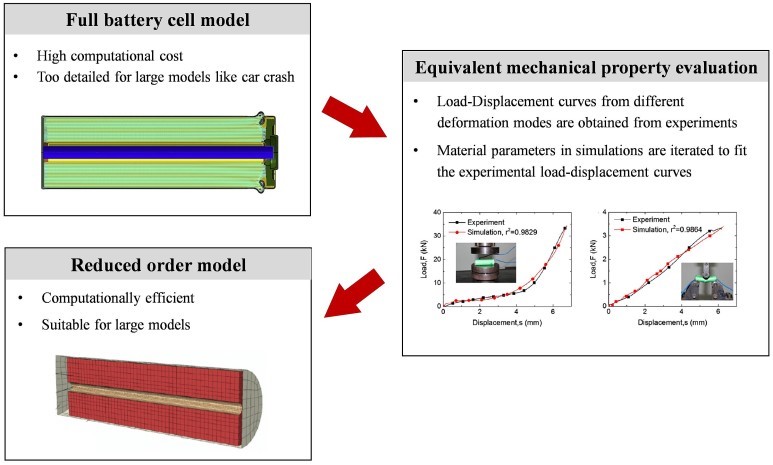
그림 2. 배터리 등가물성 도출 프로세스
다음은 젤리롤의 반경방향 압축조건(이하, 모델 1)과 3점 굽힘조건(이하, 모델 2)에서의 하중-변위 곡선(Xu. et al., 2016)을 활용하여 등가물성을 도출한 사례입니다. 해석 시간 절감을 위해 모델 1은 2D 평면변형률 모델을 활용하였고, 모델 2는 3D 1/4 대칭 모델을 활용하였습니다(그림 3.). 젤리롤의 축방향과 반경방향 이방성을 고려하기 위해 Hill 항복모델을 적용하였으며, 그림 4. 형태의 가공경화를 가정하였습니다. 재료 항복 모델 파라미터는 εo, n, A, B, m 총 5개입니다.
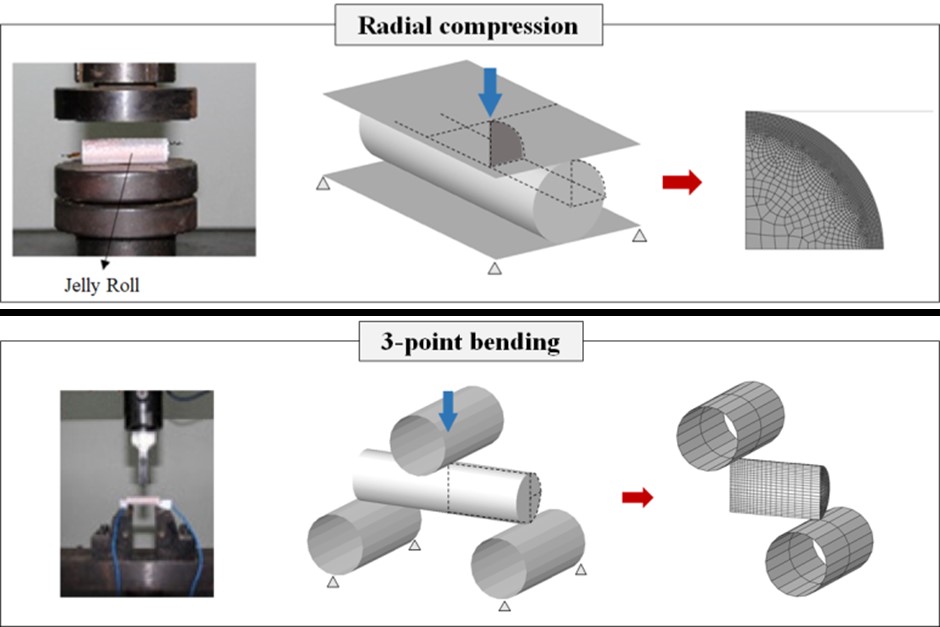
그림 3. 물성 보정을 위한 FE 해석 모델
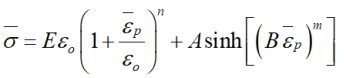
그림 4. 젤리롤 재료 항복 모델
Isight 최적화 프로세스는 그림 5.와 같이 구성됩니다. 우선, 엑셀에서 εo, n, A, B, m 5가지 변수를 이용하여 stress-strain table을 생성하고 이를 Abaqus에 전달합니다. Stress-strain curve를 적용한 두 가지 변형 모드의 해석을 수행하고 Data Matching 컴포넌트가 실험-해석 간 하중-변위 곡선의 면적 차이를 계산합니다. 이를 Optimization 컴포넌트에 전달하면 Hooke-Jeeves 최적화 알고리즘에 따라 물성 파라미터를 조절하며 위 과정을 반복해 등가물성을 도출합니다.
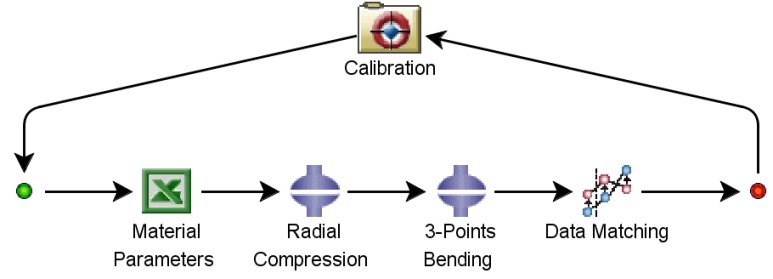
그림 5. Isight를 통한 젤리롤 등가물성 도출 프로세스
마지막으로, Isight 최적화 결과입니다. 그림 6.은 실행 횟수에 따른 실험-해석 곡선의 차이를 나타내며 반경방향 압축조건과 3점 굽힘조건 결과를 각각 나타냅니다. 초기의 실험-해석 곡선의 면적 차이값 대비 90% 정도로 상당히 감소한 것을 확인할 수 있습니다. 그림 7.은 calibration 결과이며 각각 반경방향 압축, 3점 굽힘 결과입니다. 해석 결과가 실험과 다소 차이가 발생하나 두 가지 변형 모드에 대해 대체적으로 만족스럽게 피팅된 것을 확인할 수 있습니다.
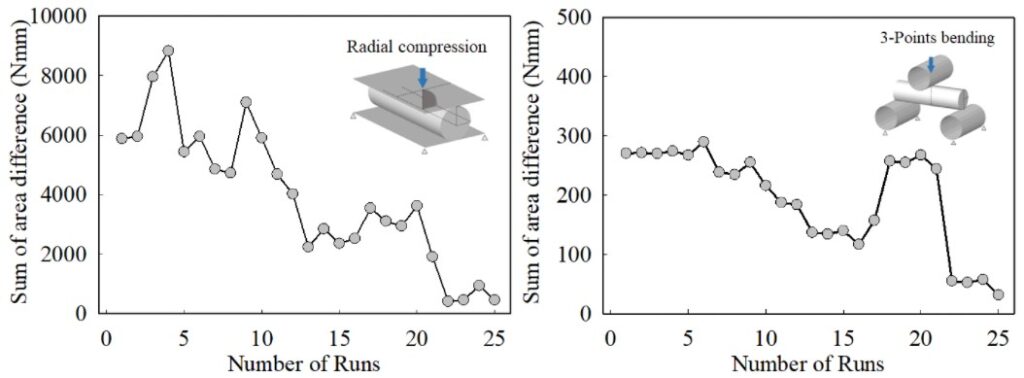
그림 6. 실행 횟수에 따른 실험-해석 간 오차(하중-변위 곡선 사이 면적 차이)
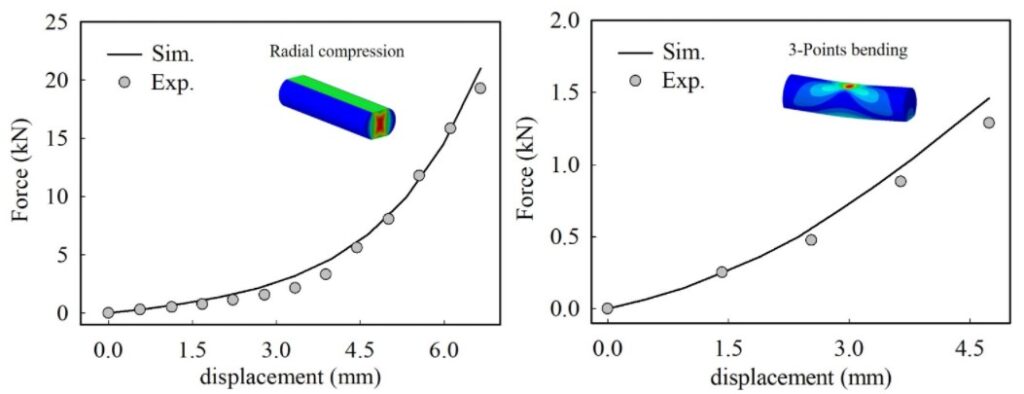
그림 7. 물성 calibration 결과와 실험 하중-변위 곡선 비교. 반경방향 압축(좌), 3점 굽힘(우)
본 포스팅에서는 재료 모델 단순화를 위해 Hill 항복 모델을 적용하여 재료 이방성만을 고려하였으나, 압력의존성 항복까지 추가로 고려한 서브루틴을 작성한다면 실험과 correlation이 더욱 개선된 등가물성 도출이 가능할 것이라 사료됩니다.