현재의 통신 환경은 한정된 주파수 자원으로 인해 Channel Capacity를 최대로 가져가기 위한 고 성능의 filter가 필수가 되었다. 이유는 제한된 주파수 spectrum을 정교하게 channel 화 해야 하기 때문이다. 고성능의 filter는 적은 삽입 손실과 높은 스커트 특성을 가지고 있는데, 삽입 손실은 신호가 필터를 통과하면서 발생하는 손실을 말하며, 스커트 특성은 통과 대역과 저지 대역이 잘 구분되는 정도를 말한다. 이에 더불어 시스템의 소형, 경량화의 요구 사항에 따라 filter의 설계 난이도는 점점 높아지고 있으며, 앞선 요구 사항에 따라 filter의 성능 최적화는 필수가 되었다.

그림 1. Cavity Filter
Cavity filter의 최적화는 filter를 구성하는 다수의 변수를 변경함으로써 이루어질 수 있다. 예를 들면, 그림 2의 single cavity filter는 6개의 변수 변경을 통해서 성능 확보가 가능한데, 이러한 다수의 변수를 일일이 변경하면서 측정을 하기에는 많은 resource가 소요된다. 다수 변수에 대한 최적화가 필요한 경우, CAE 해석을 많이 활용하는데, CST STUDIO SUITE을 활용하면 single cavity filter에 대한 최적화 뿐만 아니라, Nth order cavity filter에 대해서도 최적화 기능을 제공하고, 이에 대한 결과인 s-parameter 특성, group delay, external Q와 input coupling 대한 결과도 확인해 볼 수가 있다.

그림 2. Single cavity filter
S-parameter는 삽입 손실과 스커트 특성 확인을 위함이고, group delay는 신호 위상의 지연 정도를 파악해 볼 수 있다. 이후의 과정은 CST STUIDO SUITE의 8개 제품 중에서 CST Micro Wave Studio (MWS)와 CST Design Studio (DS)를 활용하여, cavity filter 설계 및 결과 최적화에 대한 내용을 소개하겠다.
CST MWS 내에 있는 Eigenmode Solver를 활용하면 cavity filter의 고유 공진 모드 및 전자기장 분석을 빠르게 파악할 수 있다. Eigenmode solver에서는 Advanced Krylov subspace (ASK) 방법과 Jacobi-Davidson (JDM) 방법을 통해 lossy structure의 해석을 가능케하고, 결과에 대한 효율성과 정확성을 제공하고 있다. 그림 3은 single cavity filter의 Eigenmode 분석 결과이다. Eigenmode solver를 통해서 전기장 분포와 공진주파수를 plot 할 수가 있는데, 이를 통해 filter 설계의 1차적인 결과를 확인할 수 있다. 또한 해석 후의 결과에 대한 Post-Processing 기능을 통해 filter의 Q-factor, resonance frequency도 확인할 수가 있으며, 이 내용은 그림 4에 나타내었다. Filter의 Q값은 주파수 응답 상의 첨예도를 나타내며, Q = fc / BW이다 (fc는 공진주파수, Bw는 3dB difference).
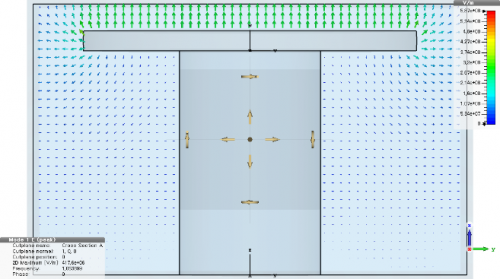
(a) 전기장 분포

(b) 공진주파수
그림 3. Single cavity filter의 (a) 전기장 분포와 (b)공진주파수

그림 4. Post-processing 기능을 이용한 Q factor와 frequency plot
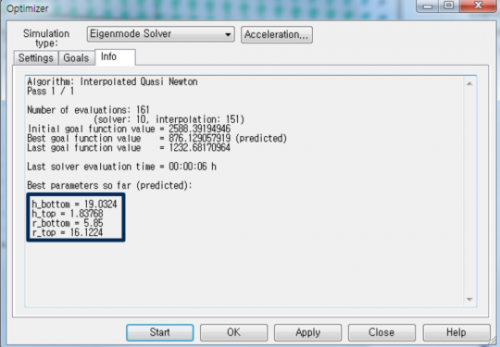
그림 5. Optimizer를 활용한 cavity filter 최적화
Q가 높을수록 더 selective 한 filter가 되며, 낮을수록 selectivity는 감소되지만 넓은 bandwidth를 가진다. 설계된 filter의 1차 결과를 확인하면 target value와 match가 되지 않는 경우가 있다. 이런 경우에 그림 5에서처럼 CST에서 제공하는 optimizer를 활용하면 target 값 match에 유용하다. Filter의 Q-factor, 공진주파수의 목표값을 설정하고, 변수로 지정한 parameter의 min / max 내에서, 목표값을 최대한 만족하는 변수값을 찾는다. 이 기능을 통해 설계자는 빠르고 정확하게 target 값 달성을 할 수 있다.
높은 스커트 특성과 넓은 bandwidth를 가지기 위해서는 Nth order filter가 필요하다. CST의 Macros 기능을 활용하면 Nth order cavity filter의 설계가 용이하다. Filter의 type은 interdigital, Combine,

그림 6. Macros 기능을 활용한 3D filter construct
Cavity-Type에 대해서 order 수, bandwidth, center frequency 등을 설정하여 construct 버튼 클릭 후에 활성화가 가능하다. 이후에 filter의 S-parameter와 Q-factor, group delay에 대한 결과 plot이 가능하다. 또한 그림 7처럼 CST DS를 이용하여, 각 port 단에 L, R, C와 같은 passive element를 연결해 특성을 파악해 볼 수 있을 뿐만 아니라, IBIS나 Touch stone 파일을 import 하여 IC의 In/Out 특성을 파악할 수 있다. IBIS 파일을 이용하면 연결된 IC의 In/out 특성을 파악할 수 있고, touch stone 파일은 component의 S-parameter 특성을 가지고 있다.

그림 7. CST DS를 활용한 circuit 구성
그림 8에서처럼 앞선 single cavity filter와 마찬가지로 optimizer 기능을 활용하여 목표치를 설정하고 지정한 변수값 변경을 통해서 목표치를 달성하는 최적의 변수값을 찾아낼 수 있다. CST를 활용하면 optimizer 외에도 변수값 변화에 따른 결과를 빠르게 살펴볼 수 있는 tune 기능도 사용할 수가 있는데, 그림 9에서 보듯이, Tune 버튼 클릭 이후에 변수로 설정해놓은 값을 변경해 볼 수 있다.
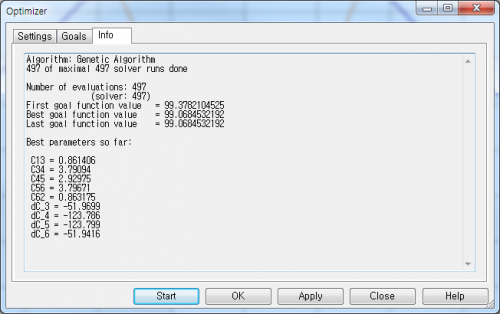
그림 8. Optimizer를 활용한 capacitor 최적화
(a) Tune 기능
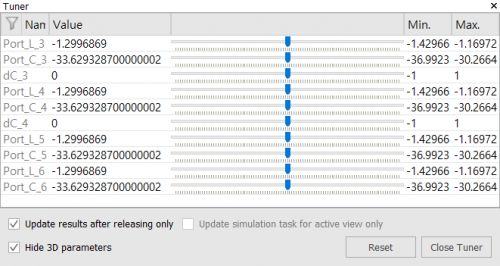
(b) Parameter 변경 창
그림 9. Tune 기능을 활용한 parameter 변경
Min / Max 값 사이에서 설계자는 값 변경에 따른 결과를 바로 확인할 수가 있기 때문에 유용하게 사용될 수 있다.
Nth order filter를 설계할 때, filter를 구성하는 parameter 변경을 하게 되면, 전체 filter의 s-parameter 변경이 일어나게 된다. 설계자가 어떤 filter가 mismatching되어 있는지를 알 수가 있다면 해당되는 filter의 parameter만을 수정하여 target을 만족할 수 있을 것이다. Nth order filter를 설계할 때 Inverse Chirp-Z Transformation을 활용하면 각 filter 단에서 matching 여부를 확인할 수 있다.

(a) Filter의 S-parameter 특성

(b) 시간영역에서의 Impedance 특성
그림 10. Inverse Chirp-Z Transformation
S-parameter 특성은 주파수 영역에서의 filter 특성을 확인하는 것이고, inverse Chirp-Z transformation은 시간 영역에서의 filter 특성을 확인한다. 그림 10(a)에서처럼, 일정한 주파수 영역(Inverse Chirp-Z bandwidth)을 선택한 뒤에, 이 특성을 확인하기 위해 Discrete Fourier Transform을 활용하면, 그림 10(b)에서처럼 시간 영역에서의 impedance 특성을 확인할 수 있다. 그림 10(b)에서 숫자로 표시된 resonance point가 각 filter의 특성을 보여주고 있다. CST에서는 post-processing 기능을 활용하여, inverse chirp Z transformation을 활용할 수 있으며, 중심 주파수 (F-center)와 bandwidth를 설정하고 T-start, T-stop을 지정하면 결과를 확인할 수 있다. 그림 11(a)에 보듯이 4th order cavity filter 설계 시에 inverse Chirp Z transformation을 활용해 볼 수가 있는데, filter의 matching 여부는 설계된 주파수에서의 dip level을 확인하는 것으로써 판단해 볼 수 있다.
그림 11(b)는 그림 11(a)의 resonator ‘1’의 tuner 길이만 변경하고 나머지 resonator의 parameter 변경은 없는 상태이다. Resonator ‘2’의 resonance가 15ns 근처에서 이루어져야 하는데 그림 11(b)를 통해서 resonator ‘2’가 mismatching 된 것을 확인할 수 있다. 그림 11(c)는 resonator ‘2’의 tuner 길이를 변경한 것이다. 그림 11(c)에서 보듯이, resonator ‘2’의 값 변경에도 첫 번째 resonator의 결과는 변하지 않는 것을 확인할 수 있다. 이처럼 Inverse Chirp-Z Transformation을 활용하면, 각 resonator의 mismatching 여부를 확인해 볼 수가 있고, 이는 설계자에게 아주 큰 장점이 될 수 있다.

(a) 4th order Cavity filter
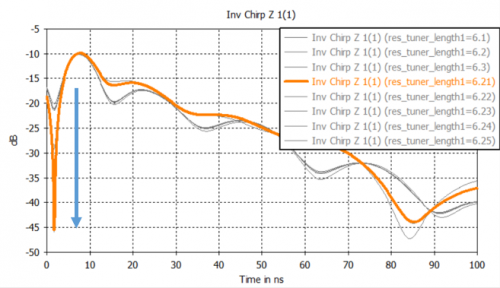
(b) Tuning of 1st resonator
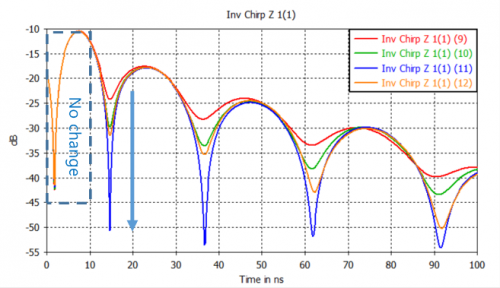
(c) Tuning of 2nd resonator
그림 11. Resonator matching에 따른 impedance 변화
지금까지 CST MWS와 CST DS를 활용하여, cavity filter의 single element부터 Nth order element의 설계에 대한 내용을 살펴보았다. 앞서 설명한 것처럼, CST MWS를 이용하면, calculator를 활용한 filter를 설계할 수가 있고, mismatching된 부분에 대해서는 tune 기능과 optimizer를 활용하여 최적화를 진행할 수 있었다. 또한 Inverse Chirp Z transformation을 통해 설계자는 mismatching filter의 확인뿐만 아니라, filter의 resonance level도 확인할 수가 있다. 또한 CST DS를 활용하여 IBIS import를 통해 IC의 in/out 특성을 파악해 볼 수가 있고, touchstone file import를 통해 s-parameter 분석도 가능하다. 이러한 CST의 기능을 활용하면 각 사업분야에 맞는 cavity filter의 설계가 용의하고 cavity filter의 설계 기간 단축 효과를 가져올 것을 생각된다. 또한 CST에서는 cavity filter뿐만 아니라, planar filter에 대해서도 설계 가능한 tool을 제공하고 있다. 이 또한 calculator를 사용하여 특성 분석을 할 수 있다.
많은 설계자들이 항상 우려하는 부분 중에 하나가 설계한 component의 측정과 시뮬레이션 결과의 일치 여부이다. Filter의 측정과 시뮬레이션 결과와의 일치를 위해서는 filter의 재질 설정 및 가공 등에서 수준 높은 기술이 요구된다. 제작상, 정밀한 오차가 요구되며, 조립에 있어서도 오차 등이 최소화되는 완벽성이 고려되어야만 요구 특성을 얻을 수가 있다. 설계자는 시뮬레이션 기법을 활용하여, 제작 후에 측정 결과와의 mismatching된 부분을 경험적으로 얻고, 이를 다시 시뮬레이션에 적용하는 단계를 거치게 될 것이다. 이 단계에서도 앞서 설명하였던 CST 기법이 유용하게 사용될 것으로 생각되며, CST를 활용하면 설계자는 많은 filter 설계에 있어서 많은 경험을 쌓을 것으로 기대된다.
