1. Introduction
최근 전기차, 수소전기차와 같은 친환경 자동차의 필요성이 증가함에 따라 배터리 성능에 대한 요구사항 역시 크게 증가하고 있습니다. 배터리 안정성은 기타 성능 대비 우선적으로 보장되어야 하며 특히 차량 충돌과 같은 극한 상황에서도 차량 배터리는 구조적 건전성을 가져야 합니다. 이에 구조해석을 통한 안정성 평가가 필수적이나, jelly-roll의 복잡한 구조 및 재료층을 그대로 모사하는 것은 해석 모델의 크기를 증대시켜 실용성이 떨어집니다. 따라서 차량 충돌해석과 같은 large scale 해석 모델에서는 연산 비용 감소를 위한 배터리셀 jelly-roll의 등가물성에 대한 연구가 활발히 이루어지고 있습니다. 본 포스팅에서는 jelly-roll의 압력의존성 소성과 항복이방성이 동시에 고려된 등가물성 도출을 위해 Hill potential을 적용한 crushable foam model을 이용하였습니다. Anisotropic crushable foam model은 Abaqus 2022 (Hot fix 1) 부터 지원하고 있으며, Standard, Explicit 두 솔버 모두에 활용 가능합니다.
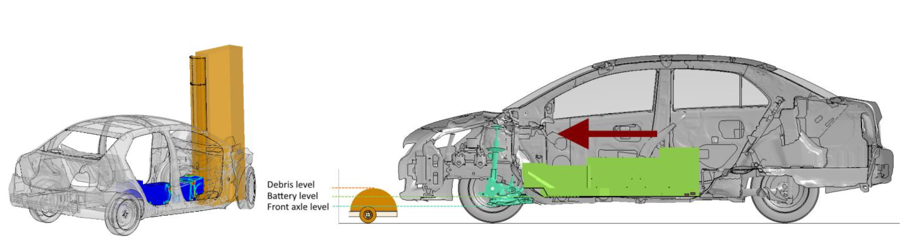
Fig. 1 Impact simulation for EV (Léost and Boljen, 2014)
2. Anisotropic crushable foam model
배터리셀 내부에 위치한 Jelly-roll 은 절연체, 음극재, 양극재, 금속포일을 엮어 와인딩 공정으로 제작되는 복합소재이며 (Fig. 2) 구조적 특성에 의해 두 가지 특징적인 소성거동을 보입니다. 첫번째는 정수압 응력에 의해 소성변형이 발생하는 압력의존성입니다. 금속재료는 정수압 응력에 의해 소성변형이 발생하지 않기 때문에 보통 Von-Mises 항복곡면을 이용하여 소성거동을 모사합니다. 반면 jelly-roll 의 경우 음극재 및 양극재에 다량의 기공이 포함되어 있기 때문에 정수압에 의해 소성변형이 발생할 수 있습니다. 두번째는 인가된 하중의 방향에 따라 항복응력이 다른 이방성 거동입니다. Fig. 2에서 볼 수 있듯이 jelly-roll은 반경방향과 축방향으로 재료의 배열이 다르며 축방향으로 더 높은 강성을 갖습니다. Abaqus 는 2022 (Hot fix 1) 버전부터 crushable foam 소성모델 (압력의존성)에 potential 옵션 (이방성)을 추가함으로서 jelly-roll 의 두 가지 특성을 동시에 고려할 수 있습니다.
소성물성 파라미터는 가공경화곡선을 모사하기 위한 5 변수 (εo, n, A, B, m), 항복곡면의 형상을 결정하기 위한 3 변수로 (kc, kt, R) 총 8개이며 (Fig. 3) 실험-해석 간 하중-변위 곡선의 차이를 최소화하는 파라미터를 Isight로 도출하였습니다. 등가물성 도출 프로세스에 대한 자세한 내용은 다쏘시스템 코리아 블로그의 이 전 포스팅을 참고하시기 바랍니다 [LINK].
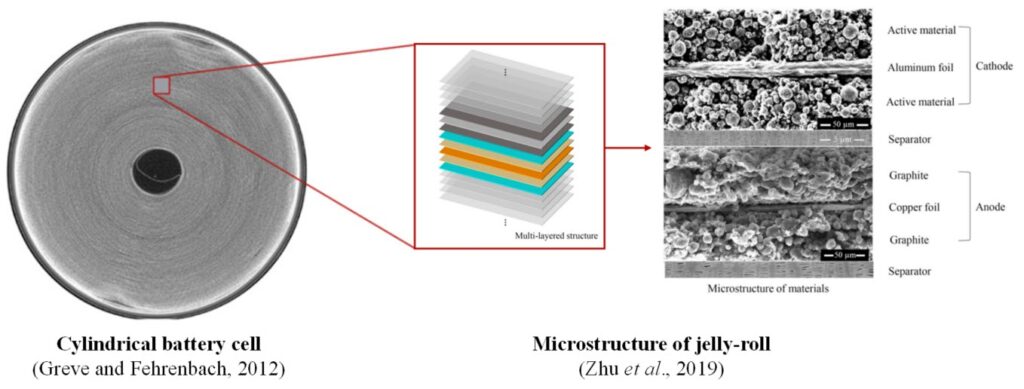
Fig. 2 Cross-section of a cylindrical battery cell and microstructure of jelly-roll

Fig. 3 Plastic parameters employed in anisotropic crushable foam model
3. Modeling
3.1 Abaqus를 이용한 FE 모델
본 포스팅에서는 jelly-roll의 등가물성을 도출하기 위해 반경방향 압축조건 (모델1)과 3-점 굽힘조건 (모델2)을 고려하였습니다. Fig. 4에서 해석 모델의 경계조건 및 하중조건을 확인할 수 있으며 해석 시간 절감을 위해 모델1과 모델2는 각각 2D 평면변형률 모델, 3D 1/4 대칭 모델을 활용하였습니다. Dynamic, Explicit 프로시저를 이용하여 준정적 해석을 수행하였으며, 운동에너지가 변형에너지의 1% 미만이 되도록 mass scaling을 적용하였습니다.
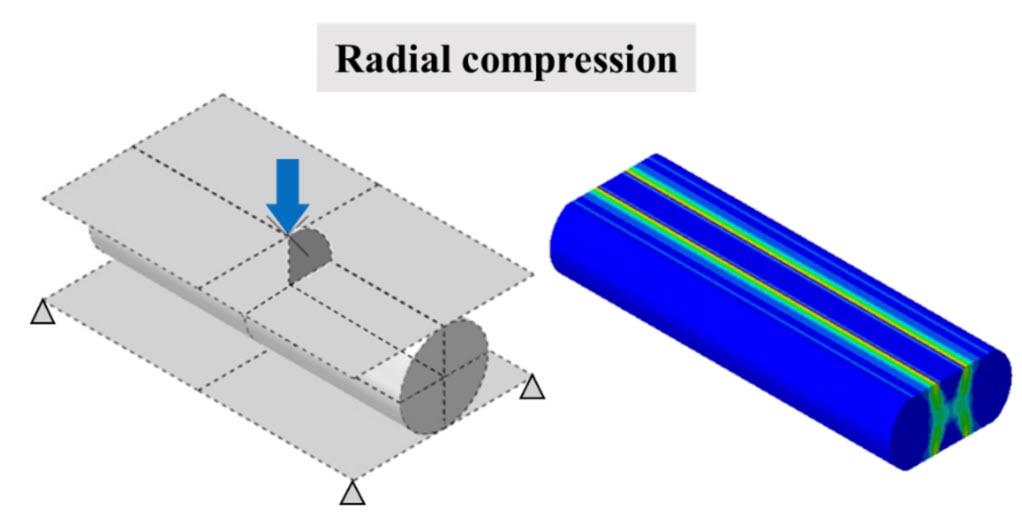
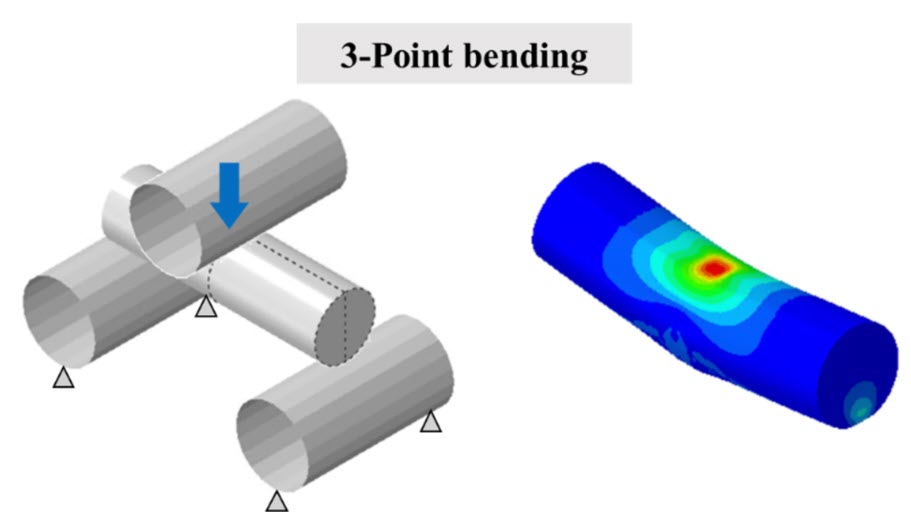
Fig. 4 Jelly-roll FE models and deformed shape
3.2 Isight를 이용한 물성 calibration 프로세스
Isight workflow는 최적화 알고리즘 초기값 설정을 위한 DOE (Design of Experiment) 루프, 물성 파라미터 calibration을 위한 Optimization 루프로 구성했습니다. DOE 루프에서는 변수공간 내에서 라틴하이퍼큐브 샘플링을 통해 20개의 parameter set 을 생성했으며 그 중, 실험-해석 간 하중-변위 곡선 차이가 가장 작게 발생하는 set 을 최적화 알고리즘의 초기값으로 적용했습니다. 최적화 알고리즘은 Hooke-Jeeves pattern search algorithm 을 적용했으며 100회 iteration 후 Loop 컴포넌트에 최적화 결과를 전달합니다. Loop 컴포넌트에서는 실험-해석 곡선 간의 면적 차이가 설정 값 이하가 되는지 확인 후 만족하지 못하면 DOE-Optimization 순의 프로세스를 반복합니다.
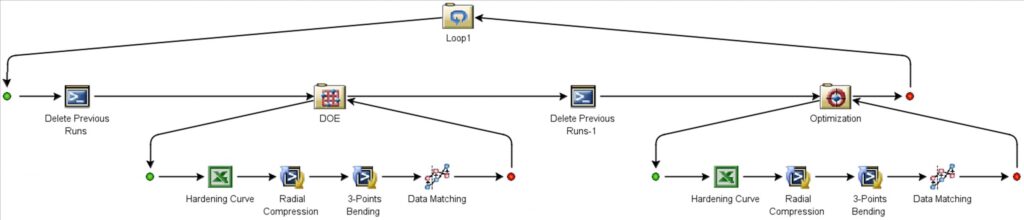
Fig. 5 Isight workflow for identification of plastic parameters for anisotropic crushable foam model
4. Results and discussion
4.1 Calibration results
Fig. 6 에서는 압력의존성과 이방성을 모두 고려한 anisotropic crushable foam 모델과, 이방성만을 고려한 모델(이하 Von-Mises 모델)의 해석결과를 실험 하중-변위 곡선과 비교하였습니다. Von-Mises 모델의 경우 지난 포스팅의 calibration 결과를 활용하였으며 6 개의 재료변수를 (εo, n, A, B, m, R) 사용하였습니다[LINK]. 두 소성모델 모두 jelly-roll 의 반경방향 압축과 3-점 굽힘조건에 대해서 calibration이 잘 수행되었음을 확인할 수 있습니다.
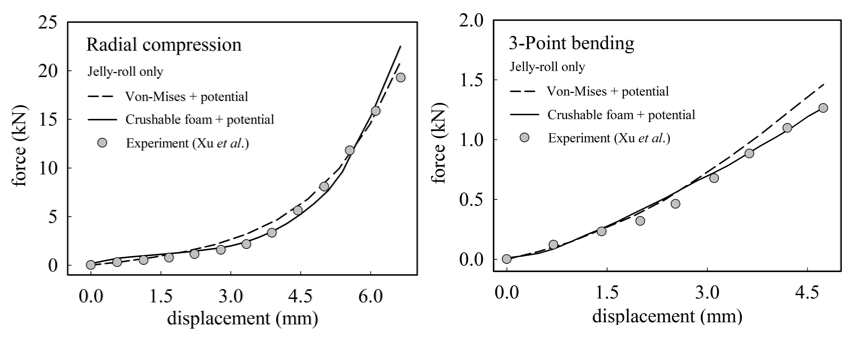
Fig. 6 Comparison of calibrated force-displacement curve for two plasticity models and experiment
4.2 Validation
도출한 jelly-roll 등가물성은 cell casing 을 포함한 3D 모델의 실험-해석 간 하중-변위 곡선을 비교해 검증했습니다. 도출한 등가물성이 타당하려면 calibration에 사용된 하중조건 외의 변형모드에서도 실험과 유사한 거동을 보여야 합니다. 따라서 등가물성 검증을 위해 압입 (Indentation) 하중조건을 추가하으며, Fig. 7 에 두 소성모델의 하중-변위 곡선 예측 결과를 실험과 비교했습니다. 비교 결과, 반경방향 압축과 압입조건은 압력의존성과 이방성 모두 고려한 crushable foam 모델의 결과가 실험과 더 높은 correlation을 보입니다. 3-점 굽힘의 경우 두 모델 간 차이가 거의 발생하지 않았는데, 이는 해당 변형모드에서 정수압 응력 성분이 미미하여 압력의존성 영향이 작기 때문인 것으로 보입니다.

Fig. 7 Validation of identified material parameters with 3D FE results
5. Conclusion
본 포스팅에서는 Abaqus 2022 업데이트 기능인 anisotropic crushable foam 모델을 활용하여 배터리셀의 등가물성을 도출하였습니다. 등가물성 도출에는 jelly-roll 의 반경방향 압축과 3-점 굽힘 실험데이터를 이용하였고 연산시간 단축을 위해 2D 모델 및 3D 대칭모델을 사용했습니다. 마지막으로 cell casing 을 포함한 3D 해석을 3가지 변형모드에 대해 수행했고 실험 하중-변위 곡선과 비교하여 도출물성을 검증했습니다. Jelly-roll 의 소성 특성인 압력의존성과 항복이방성을 모두 고려할 경우, 실험-해석 간 correlation이 더욱 개선된 현실적인 등가물성 도출이 가능함을 확인했습니다. 기존에는 jelly-roll 의 두 가지 특성을 반영하기 위해 별도의 유저 서브루틴 작성이 필요했으나 최신버전에서는 built-in material 로 제공하고 있기 때문에 보다 적용이 편리해졌습니다. 본 포스팅에 대한 문의는 다쏘시스템 기술지원 팀으로 연락주시기 바랍니다 (02-3270-8541, SIMULIA.KR.Support@3ds.com).
References
Abaqus Documentation, 2022, Dassault Systèmes Simulia Corp., Providence, RI, USA.
Greve L, Fehrenbach C, 2012, Mechanical testing and macro-mechanical finite element simulation of the deformation, fracture, and short circuit initiation of cylindrical Lithium ion battery cells, Journal of Power Sources 214, 377 − 385.
Léost Y, Boljen M, 2014, Crash simulations of electric cars in the eversafe project, XIII International Conference on Computational Plascity : Fundamentals and Applications, COMPLAS XIII, Barcelona.
Wang L, Yin S, Xu J, 2019, A detailed computational model for cylindrical lithium-ion batteries under mechanical loading: From cell deformation to short-circuit onset, Journal of Power Sources 413, 284 – 292.
Xu J, Liu B, Wang X, Hu D, 2016, Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies, Applied Energy 172, 180 -189.
Zhu J, Zhang X, Sahraei E, Tomasz W, 2016, Deformation and failure mechanisms of 18650 battery cells under axial compression, Journal of Power Sources 336, 332 -340.
Zhu J, Wierzbicki T, Li W, 2018, A review of safety-focused mechanical modeling of commercial lithium-ion batteries, Journal of Power Sources 378, 153 – 168.
